Research

Working papers

• Optimal tradeoffs between variance and sensitivity, via Hellinger–Kantorovich geometry with Congwei Yang, Nicolás García Trillos, and Bodhisattva Sen.
  
• Total variation information geometry and robust statistics with Dohyeong Ki and Bodhisattva Sen.
  
• Phylogenetic inference and the stickiness of Fréchet means, via precise asymptotics of an embedded random walk.
  Submitted (2026+)
  [abstract] [animation] [arxiv] [code]

• 

• A well-known phenomenon in statistical analyses of populations of phylogenetic trees in the Billera-Holmes-Vogtmann space is that the topology of the Fréchet mean tree can contain multifurcations (i.e., internal nodes with more than two children), which raises the practical question of whether this reflects a population-level branching structure (hard polytomy) or merely sampling variability in the data (soft polytomy). This is an instance of the more general phenomenon of ``stickiness'' in non-Euclidean statistics, whereby the sample Fréchet mean in certain non-positively curved stratified spaces becomes permanently trapped in a lower-dimensional stratum. In this work, we identify a particular multidimensional random walk embedded within the Fréchet mean process, and we show that the time at which stickiness occurs coincides with the largest last-passage time above zero of the coordinates of this random walk. Using this representation, we develop a fully nonparametric procedure for estimating the probability that trifurcations in a sample Fréchet mean tree will eventually bifurcate if more observations are collected. Lastly, we apply our methodology to a problem in phylogenetics where we consider whether an observed trifurcation in the species tree of primates, glires, and tree shrews is genuinely trifurcated at the population-level.
• Coupling theory, optimal transport, and Strassen's theorem for eventual domination with Daniel Raban.
  Submitted (2026+).
  [abstract] [arxiv]
• Many results in probability (most famously, Strassen's theorem on stochastic domination), characterize some relationship between probability distributions in terms of the existence of a particular structured coupling between them. Optimal transport, and in particular Kantorovich duality, provides a framework for formally unifying these results, but the standard duality theory requires topological conditions that are not satisfied in some settings. In this work, we investigate the extent to which Kantorovich duality still provides meaningful connections between distributional relations and their coupling counterparts, in the topologically irregular setting. Towards this end, we show that Strassen's theorem "nearly holds" for topologically irregular orders but that the full theorem admits counterexamples. The core of the proof is a novel technical result in optimal transport, which shows that the Kantorovich dual problem is well-behaved for optimal transport problems whose cost functions can be written as a non-increasing limit of lower semi-continuous functions.




In revision

• Nonparametric Riemannian empirical Bayes, denoising measurements on manifolds with Leonardo Santoro and Bodhisattva Sen
  Major revision, Annals of Statistics.
  [abstract] [arxiv] [code]
• We initiate the study of nonparametric empirical Bayes denoising methods in the setting where both the latent variables and their measurements lie on a compact Riemannian manifold, and where the likelihood is a Riemannian Gaussian distribution. Our starting point is a novel Tweedie-Eddington formula for Riemannian Gaussian mixture models which identifies a certain surrogate oracle denoiser in terms of the marginal distribution of the measurements; it avoids the explicit computation of the posterior Fréchet mean (as required by the Bayes denoiser) via a first-order approximation, hence we refer to it as the "tangential" Bayes denoiser. We show that this surrogate oracle achieves nearly the Bayes risk in a low-noise regime, we construct a fully data-driven approximation of it using the spectral theory of the Laplace-Beltrami operator, and we establish finite-sample rates of convergence for the distance between the the surrogate oracle and its approximation. Contrasting the nearly-parametric rates from the Euclidean setting, the rates in the Riemannian setting are slower due to the singularities of the Riemannian Gaussian density at the cut locus of its Fréchet mean; in the special case of the circle we establish matching lower bounds which show that our proposed denoiser is minimax-optimal, and that the denoising problem exhibits a genuinely nonparametric rate of convergence. Our theory and simulations reveal that pooling information across different measurements—namely, by shrinking towards high-density regions and stretching away from low-density regions—can substantially outperform the naïve denoiser that treats each measurement separately. Lastly, we implement our methodology in two scientific applications: in astronomy, the sphere-valued problem of denoising the locations of gamma ray bursts; in structural biology, the torus-valued problem of denoising pairs of torsion angles of adjacent amino acids in a protein (i.e., the Ramachandran plot).
• Wasserstein-Cramér-Rao theory of unbiased estimation with Nicolás García Trillos and Bodhisattva Sen
  Major revision, Annals of Statistics.
  [abstract] [arxiv]
• The quantity of interest in the classical Cramér-Rao theory of unbiased estimation (e.g., the Cramér-Rao lower bound, its exact attainment for exponential families, and asymptotic efficiency of maximum likelihood estimation) is the variance, which represents the instability of an estimator when its value is compared to the value for an independently-sampled data set from the same distribution. In this paper we are interested in a quantity which represents the instability of an estimator when its value is compared to the value for an infinitesimal additive perturbation of the original data set; we refer to this as the "sensitivity" of an estimator. The resulting theory of sensitivity is based on the Wasserstein geometry in the same way that the classical theory of variance is based on the Fisher-Rao (equivalently, Hellinger) geometry, and this insight allows us to determine a collection of results which are analogous to the classical case: a Wasserstein-Cramér-Rao lower bound for the sensitivity of any unbiased estimator, a characterization of models in which there exist unbiased estimators achieving the lower bound exactly, and some concrete results that show that the Wasserstein projection estimator achieves the lower bound asymptotically. We use these results to treat many statistical examples, sometimes revealing new optimality properties for existing estimators and other times revealing entirely new estimators.
• Constrained denoising, empirical Bayes, and optimal transport with Nikolaos Ignatiadis and Bodhisattva Sen.
  Major revision, Journal of the Royal Statistical Society Ser B.
  [abstract] [arxiv] [code]
• In latent variables models, two important goals are denoising and deconvolution: denoising aims to estimate the latent variables, whereas deconvolution aims to estimate the distribution of the latent variables. As has been recognized in the literature over the last century, these two goals are fundamentally in tension, since denoising yields a poor estimate of the distribution of the latent variables due to shrinkage, and deconvolution yields a distribution-valued estimate that carries no unit-specific information. In this paper, we provide a systematic study of denoisers, and empirical Bayes approximations thereof, which attain optimal denoising error subject to the constraint that the distribution of the denoised data matches, in some sense, the distribution of the latent variables. Our insight is that optimal transport allows practitioners to navigate the tension between denoising and deconvolution. More precisely, we propose a modular methodology that combines any suitable unconstrained empirical Bayes denoiser (arising, e.g., via $F$-modeling, $G$-modeling, conjugate-parametric models) with any suitable information about the distribution of the latent variables (e.g., its moments, support, or an approximation of the entire distribution via deconvolution) into a single denoised data set. We prove explicit rates of convergence for our proposed methodologies, and we apply the resulting methods in applications in astronomy, baseball analytics, and marketing.
• Fréchet means in infinite dimensions.
  Minor revision, SIAM Journal on Mathematical Analysis.
  [abstract] [arxiv]
• While there exists a well-developed asymptotic theory of Fréchet means of random variables taking values in a general "finite-dimensional" metric space, there are only a few known results in which the random variables can take values in an "infinite-dimensional" metric space. Presently, we develop a general asymptotic theory of Fréchet means in some infinite-dimensional metric spaces, which allows us to recover, strengthen, and generalize most existing results; in particular, we develop novel asymptotic theory for Fréchet means in some infinite-dimensional metric spaces from statistical shape analysis. The core of the proof is a novel notion of weak convergence in general metric spaces for which the results can be proven via calculus of variations.
• Large deviations principle for Bures-Wasserstein barycenters with Leonardo Santoro.
  Major revision, Annals of Applied Probability.
  [abstract] [arxiv]
• We prove the large deviations principle for empirical Bures-Wasserstein barycenters of independent, identically-distributed samples of covariance matrices and covariance operators. As an application, we explore some consequences of our results for the phenomenon of dimension-free concentration of measure for Bures-Wasserstein barycenters. Our theory reveals a novel notion of exponential tilting in the Bures-Wasserstein space, which, in analogy with Cramér's theorem in the Euclidean case, solves the relative entropy projection problem under a constraint on the barycenter. Notably, this method of proof is easy to adapt to other geometric settings of interest; with the same method, we obtain large deviations principles for empirical barycenters in Riemannian manifolds and the univariate Wasserstein space, and we obtain large deviations upper bounds for empirical barycenters in the general multivariate Wasserstein space. In fact, our results are the first known large deviations principles for Fréchet means in any non-linear metric space.




Publications

• Consistency and inconsistency in \(k\)-means clustering with Moïse Blanchard and Nikita Zhivotovskiy.
  Electronic Journal of Statistics. 20(2): 3291-3334.
  [abstract] [animation] [arxiv] [journal]
• A celebrated result of Pollard proves asymptotic consistency for \(k\)-means clustering when the population distribution has finite variance. In this work, we point out that the population-level \(k\)-means clustering problem is, in fact, well-posed under the weaker assumption of a finite expectation, and we investigate whether some form of asymptotic consistency holds in this setting. As we illustrate in a variety of negative results, the complete story is quite subtle; for example, the empirical \(k\)-means cluster centers may fail to converge even if there exists a unique set of population \(k\)-means cluster centers. A detailed analysis of our negative results reveals that inconsistency arises because of an extreme form of cluster imbalance, whereby the presence of outlying samples leads to some empirical \(k\)-means clusters possessing very few points. We then give a collection of positive results which show that some forms of asymptotic consistency, under only the assumption of finite expectation, may be recovered by imposing some a priori degree of balance among the empirical \(k\)-means clusters.

• 

• Asymptotic theory of geometric and adaptive \(k\)-means clustering. Annals of Statistics. 53(4): 1559-1586.
  [abstract] [arxiv] [journal]
• We revisit Pollard's classical result on consistency for \(k\)-means clustering in Euclidean space, with a focus on extensions in two directions: first, to problems where the data may come from interesting geometric settings (e.g., Riemannian manifolds, reflexive Banach spaces, or the Wasserstein space); second, to problems where some parameters are chosen adaptively from the data (e.g., \(k\)-medoids or elbow-method \(k\)-means). Towards this end, we provide a general theory which shows that all clustering procedures described above are strongly consistent. In fact, our method of proof allows us to derive many asymptotic limit theorems beyond strong consistency. We also remove all assumptions about uniqueness of the set of optimal cluster centers.
• Fréchet mean set estimation in the Hausdorff metric, via relaxation with Moïse Blanchard. Bernoulli. 31(1), 432-456.
  [abstract] [arxiv] [code] [journal]
• T This work resolves the following question in non-Euclidean statistics: Is it possible to consistently estimate the Fréchet mean set of an unknown population distribution, with respect to the Hausdorff metric, when given access to independent identically-distributed samples? Our affirmative answer is based on a careful analysis of the "relaxed empirical Fréchet mean set estimators" which identify the set of near-minimizers of the empirical Fréchet functional and where the amount of "relaxation" vanishes as the number of data tends to infinity. On the theoretical side, our results include exact descriptions of which relaxation rates give weak consistency and which give strong consistency, as well as a description of an estimator which (assuming only the finiteness of certain moments and a mild condition on the metric entropy of the underlying metric space) adaptively finds the fastest possible relaxation rate for strongly consistent estimation. On the applied side, we consider the problem of estimating the set of Fermat-Weber points of an unknown distribution in the space of equidistant trees endowed with the tropical projective metric; in this setting, we provide an algorithm that provably implements our adaptive estimator, and we apply this method to real phylogenetic data.
• Constructing maximal germ couplings of Brownian motions with drift with Sebastian Hummel. Electronic Communications in Probability. 29, 1-11.
  [abstract] [animation] [arxiv] [journal]

• 

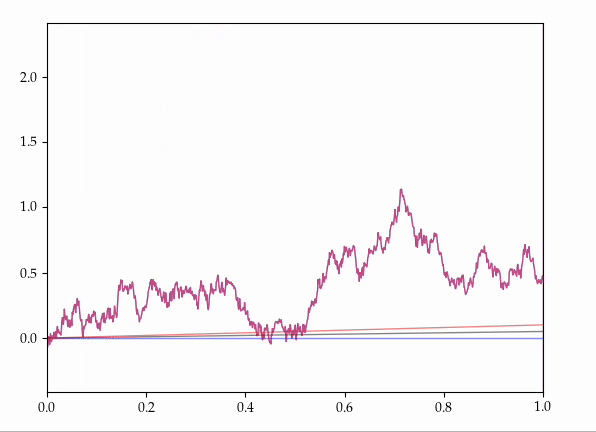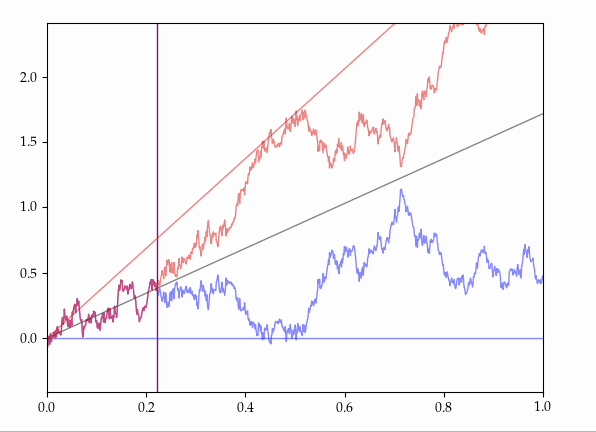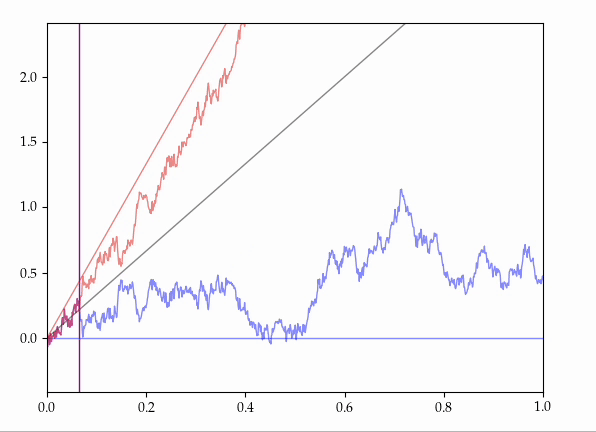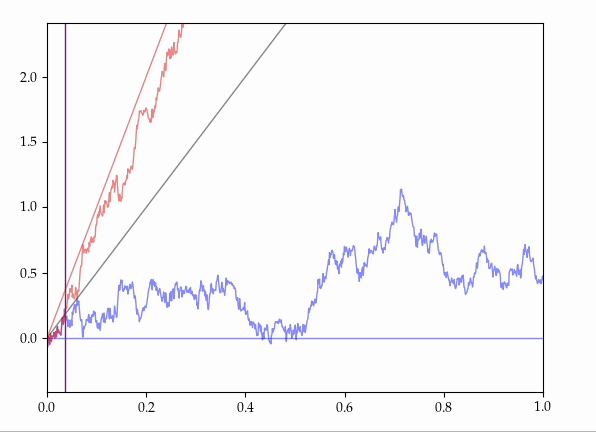
• Consider all the possible ways of coupling together two Brownian motions with the same starting position but with different drifts onto the same probability space. It is known that there exist couplings which make these processes agree for some random, positive, maximal initial length of time. Presently, we provide an explicit, elementary construction of such couplings.
• Limit theorems for Fréchet mean sets with Steve N. Evans. Bernoulli. 30(1), 419-447.
  [abstract] [arxiv] [journal]
• For \(1\le p \le \infty\), the Fréchet \(p\)-mean of a probability measure on a metric space is an important notion of central tendency that generalizes the usual notions in the real line of mean (\(p=2\)) and median (\(p=1\)). In this work we prove a collection of limit theorems for Fréchet means and related objects, which, in general, constitute a sequence of random closed sets. On the one hand, we show that many limit theorems (a strong law of large numbers, an ergodic theorem, and a large deviations principle) can be simply descended from analogous theorems on the space of probability measures via purely topological considerations. On the other hand, we provide the first sufficient conditions for the strong law of large numbers to hold in a \(T_2\) topology (in particular, the Fell topology), and we show that this condition is necessary in some special cases. We also discuss statistical and computational implications of the results herein.
• A strong duality principle for equivalence couplings and total variation. Electronic Journal of Probability. 28, 1-33
  [abstract] [arxiv] [journal]
• We introduce and study a notion of duality for two classes of optimization problems commonly occurring in probability theory. That is, on an abstract measurable space \((\Omega,\mathcal{F})\), we consider pairs \((E,\mathcal{G})\) where \(E\) is an equivalence relation on \(\Omega\) and \(\mathcal{G}\) is a sub-\(\sigma\)-algebra of \(\mathcal{F}\); we say that \((E,\mathcal{G})\) satisfies "strong duality" if \(E\) is \((\mathcal{F}\otimes\mathcal{F})\)-measurable and if for all probability measures \(\mathbb{P},\mathbb{P}'\) on \((\Omega,\mathcal{F})\) we have \[ \max_{A\in\mathcal{G}}\vert \mathbb{P}(A)-\mathbb{P}'(A)\vert = \min_{\tilde{\mathbb{P}}\in\Pi(\mathbb{P},\mathbb{P}')}(1-\tilde{\mathbb{P}}(E)), \] where \(\Pi(\mathbb{P},\mathbb{P}')\) denotes the space of couplings of \(\mathbb{P}\) and \(\mathbb{P}'\), and where "max" and "min" assert that the supremum and infimum are in fact achieved. The results herein give wide sufficient conditions for strong duality to hold, thereby extending a form of Kantorovich duality to a class of cost functions which are irregular from the point of view of topology but regular from the point of view of descriptive set theory. The given conditions recover or strengthen classical results, and they have novel consequences in stochastic calculus, point process theory, and random sequence simulation.
• Virtual Markov chains with Steve N. Evans. New Zealand Journal of Mathematics (Vaughan Jones Memorial Issue). 52, 511–559.
  [abstract] [arxiv] [journal]
• We introduce the space of virtual Markov chains (VMCs) as a projective limit of the spaces of all finite state space Markov chains (MCs), in the same way that the space of virtual permutations is the projective limit of the spaces of all permutations of finite sets. We introduce the notions of virtual initial distribution (VID) and a virtual transition matrix (VTM), and we show that the law of any VMC is uniquely characterized by a pair of a VID and VTM which have to satisfy a certain compatibility condition. Lastly, we study various properties of compact convex sets associated to the theory of VMCs, including that the Birkhoff-von Neumann theorem fails in the virtual setting.